Utilization of Complex Number and its Characteristics
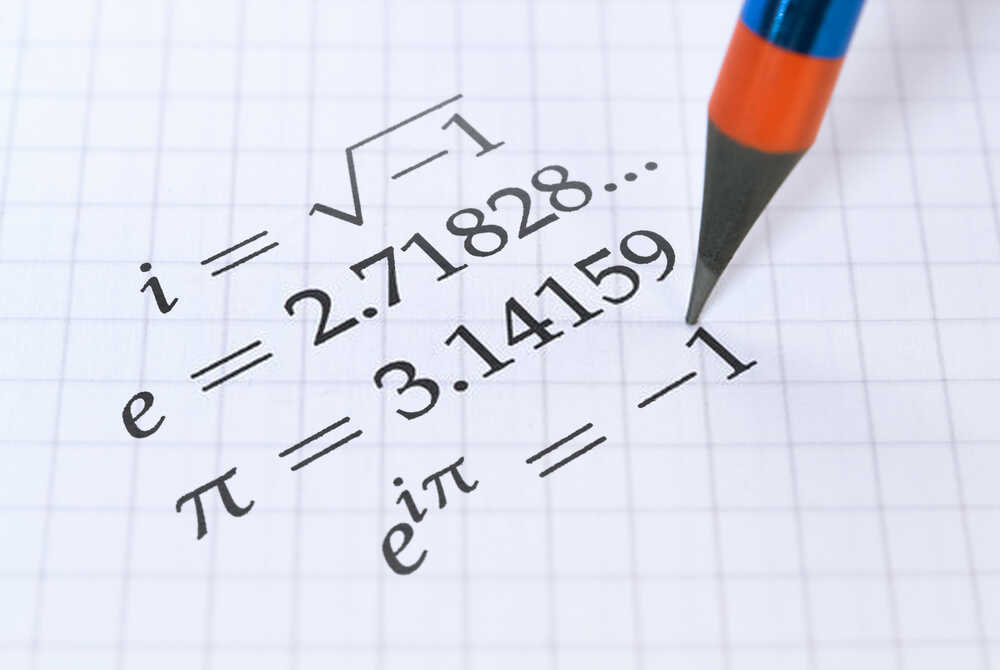
Complex number is generally presented to secondary school students in a somewhat confusing way. Till a specific grade they are informed that the square root of a negative real number is “prohibited”, and afterward i=square root of {-1} is presented out of nowhere. It is a pity that regardless of having the option to take care of a huge load of issues, most students can’t see complex numbers past simple algebraic calculations.
The real capability of complex number is maybe better understood through a mathematical perspective, trailed by its applications in different subjects like trigonometry, geometry, polynomials, combinatorics, etc. Experts have personally observed this way to be more natural, and have been using it to help a lot of students. We don’t actually have a clue how successful these tests have been, however, we can see that the students do merit using this.
Evolution of Complex Numbers
Since the square of a real number is rarely negative, there is no real number x to such an extent that x2 = – 1. Mathematicians needed this condition to have an answer. In this manner, they characterized ‘i’ to be the arrangement of the situation x2 = – 1 and called ‘an imaginary number or nonexistent unit. By doing this, they created another arrangement of numbers called complex numbers.
What they essentially did is this:
Assuming x2= – 1, Therefore, x = √-1
Let √-1 = imaginary number = I since such a number doesn’t exist with real numbers, however, exist just in our creative mind. Then, at that point, we can simply call it a complex number. Presently we utilize complex numbers in electromagnetism, signal handling, and numerous other activities.
What difference do they make?
The invention of complex numbers is critical in Algebra. To completely see the value in this, we should think about our number system, something that numerous students are rarely educated with. At first, people used normal numbers {1,2,3… } to count natural objects-for instance, 15eggs or 2 mangoes etc. Numbers were then found to comprehend concepts like debts. Integers broadened the numeral system and the natural numbers were a subset of the integers.
The following extension of the number system was the invention of rational numbers, which are characterized as the ratio of two integers. The number system was once more stretched out through the presentation of the real numbers, a set that contained both the rational and irrational numbers. Mathematicians imagined that the number system was finished and that Algebra was currently perceived. Eventually, the revelation of the complex numbers uncovered the deficiency of the number system. Truth be told, the complex numbers were the last expansion of the number system and are what is known as the algebraic conclusion of the number system. They helped with traditional algebra.
Another arrangement of numbers totally dependent on the imaginary unit i: Since i = √-1, we would then be able to denote the square root of any negative number as a real multiple of i. For instance, √-49 = √(49 × – 1) = √49 × √-1 = 7i
As a general rule, for any positive real number a, √(- a) = (√a) x i
Read Also: Which Career is the Best After 12th Science?
What is the distinction between a complex number and an imaginary number?
Let us take the complex number a + bi. In case a is not equal to 0 and b = 0, the complex number a + 0i = a and a will be a real number. Hence, all real numbers are likewise complex numbers. In case b isn’t equal to 0 and a is any real number, the complex number a + bi is called an imaginary number.
As such, if the imaginary unit ‘i’ is in it, we can simply call it an imaginary number.
Get in touch with us at the Cuemath website for more details and lessons on mathematics.






